Ma trận và vector với NumPy
Machine Learning cơ bản với NumPy
Danh sách bài học
Ma trận và vector với NumPy
Dẫn nhập
Trong bài trước, Kteam đã GIỚI THIỆU MACHINE LEARNING VÀ CÀI ĐẶT NUMPY , giúp các bạn một phần hiểu được bản chất của Machine Learning.
Ở bài này chúng ta sẽ cùng nhau tìm hiểu về Ma trận và vector với NumPy. Với bài này, Kteam sẽ giới thiệu đến các bạn một nội dung khá “toán học”, vì thế nếu cảm thấy mệt mỏi, hoa mắt, chóng mặt, trời đất quay cuồng thì hãy nghĩ ngơi một lúc 😊
Lưu ý: Một số nội dung được trình bày trong video vẫn có thể chưa hoàn toàn chính xác. Vì vậy, sau khi tham khảo góp ý từ cộng đồng , Kteam đã có hiệu chỉnh học liệu và cách diễn đạt các định nghĩa trong bài viết để nội dung có thể đi sát hơn với các tài liệu toán học.
Nội dung
Để theo dõi bài này tốt nhất bạn cần có kiến thức về:
Trong bài này chúng ta sẽ cùng tìm hiểu về:
- Định nghĩa ma trận và vector
- Cách khởi tạo ma trận và vector
- Các toán tử với ma trận
- Identify matrix và Transpose matrix
- Ý nghĩa của ma trận và vector trong Machine Learning
Ma trận (matrix) với NumPy
Định nghĩa
Ma trận là một mảng 2 chiều. Trong Python mảng 2 chiều có thể xem là một List của List.
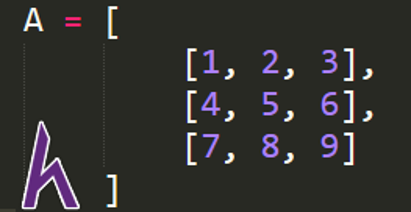
Kích thước
Kích thước của 1 ma trận = số hàng * số cột.
Ví dụ:
Ma trận B có 4 hàng và 3 cột: ma trận 4 x 3
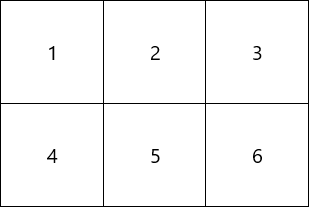
Bạn cũng có thể hiểu ma trận là một sheet với số hàng và số cột nhất định trong excel.
Vector với NumPy
Định nghĩa
Vector là ma trận với 1 cột và nhiều hàng (n * 1)
Kích thước
Kích thước của vector (còn được gọi là chiều vector – vector dimension) là số hàng của vector.
Ví dụ:
- Vector có 4 hàng là vector 4 chiều.
- Vector tương tự như 1 cột trong excel với số hàng nhất định.
Khởi tạo ma trận và vector với NumPy
Khởi tạo ma trận
Ta có thể khởi tạo ma trận với NumPy bằng np.array:
np.array(object, dtype=None, ndmin=0)
Trong đó:
- Object: một mảng 2 chiều, ta có thể sử dụng một list của list.
- dtype: kiểu dữ liệu của các phần tử trong ma trận
- ndmin: số chiều tối thiểu khi return object, nên đặt = 2 để tiện cho việc indexing ma trận cho Machine Learning.
Lưu ý: trừ object, các parameter khác khi truyền vào phải có key_arg.
Ví dụ:
import numpy as np #import numpy and uses shorter keyword
_A = [ [1, 2, 3], [4, 5, 6] ] #array-like object
A = np.array(_A) #create a 2-dimension array (matrix) from _A
print(A) #print matrix A
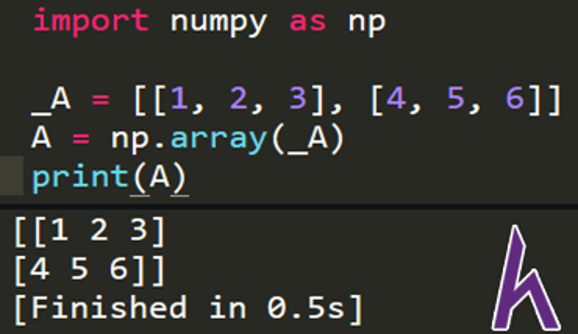
Ma trận này cũng tương tự như bảng sau:
Khởi tạo vector
Ta khởi tạo vector như ma trận nhưng chỉ có 1 cột (mảng 1 chiều). Ta có thể xem đây là 1 List.
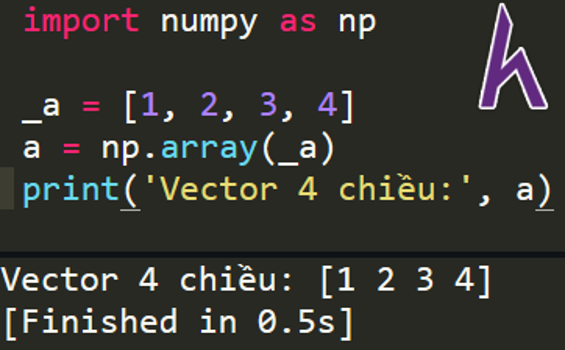
import numpy as np #import numpy and uses shorter keyword
_a = [ 1, 2, 3, 4 ] #array-like object
a = np.array(_a) #create a 1-dimension array (vector) from _a
print(‘Vector 4 chiều:’, a) #print vector a
Ví dụ:
Indexing ma trận và vector
Ta có thể indexing ma trận và vector theo cấu trúc:
Matrix_name[row_index, column_index]
Trong đó:
- Row_index, column_index có thể là kí tự ‘:’ với ý nghĩa lấy toàn bộ những phần tử theo hàng/ cột.
Ví dụ:
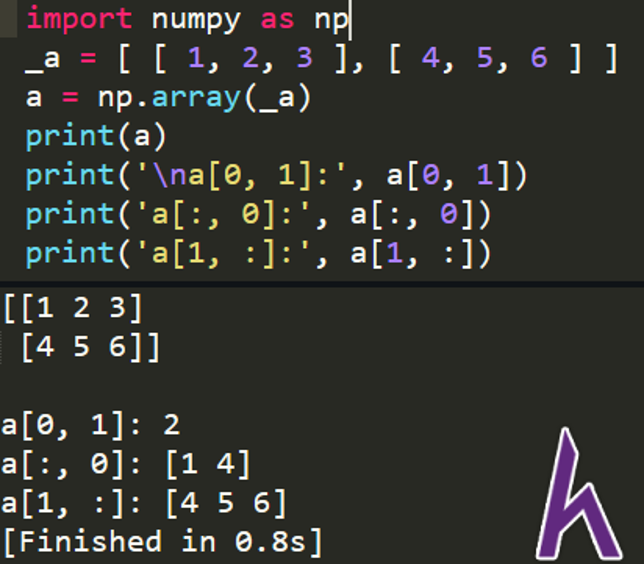
import numpy as np #import numpy and uses shorter keyword
_a = [ [ 1, 2, 3 ], [ 4, 5, 6 ] ] #array-like object
a = np.array(_a) #create a 2-dimension array (matrix) from _a
print(‘a[0, 1]:’, a[0, 1]) #print a[0, 1] element
print(‘a[:, 0]:’, a[:, 0]) #print a[:, 0] elements
print(‘a[1, :]:’, a[1, :]) #print a[1, :] elements
Các toán tử với ma trận và vector
Cộng và trừ với ma trận
Các phép toán cộng và trừ với ma trận là phép toán “element-wise”, nghĩa là phép toán với từng phần tử tương ứng.
Tương tự với trừ:
Lưu ý: Để cộng và trừ 2 ma trận, kích thước của cả hai phải giống nhau.
Ví dụ :
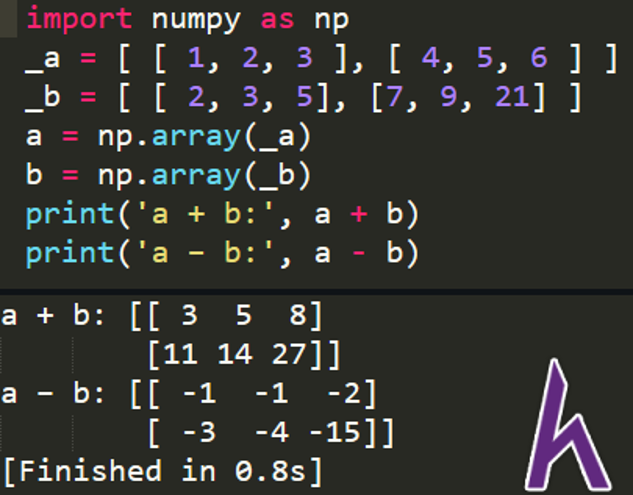
import numpy as np
_a = [ [ 1, 2, 3 ], [ 4, 5, 6 ] ]
_b = [ [ 2, 3, 5], [7, 9, 21] ]
a = np.array(_a) #create 2 * 3 matrix: a
b = np.array(_b) #create 2 * 3 matrix: b
print(‘a + b:’, a + b) #print out a + b
print(‘a – b:’, a – b) #print out a - b
Nhân và chia ma trận với số
Để nhân và chia ma trận với số, ta chỉ cần nhân/chia từng phần tử của ma trận với số đó.
Tương tự với chia:
Ví dụ:
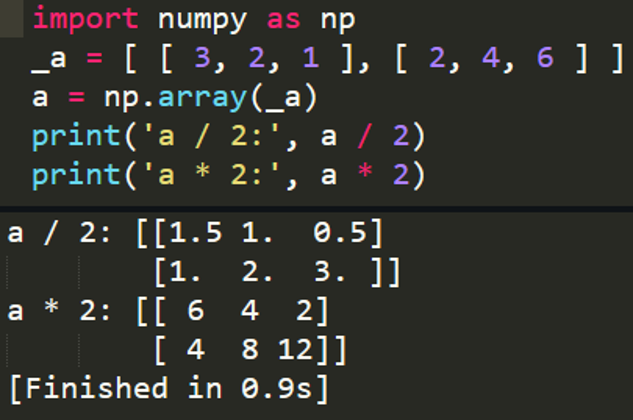
import numpy as np
_a = [ [ 3, 2, 1 ], [ 2, 4, 6 ] ]
a = np.array(_a)
print(‘a / 2:’, a / 2) #print out a / 2
print(‘a * 2:’, a * 2) #print out a * 2
Nhân ma trận với vector
Khi nhân ma trận với vector, ta lấy các phần tử trong cột số của vector nhân lần lượt với các hàng của ma trận để được các tích, sau đó lấy tổng của các tích rồi cho vào từng hàng của kết quả. Chúng ta có thể hình dung như sau:
Kết quả của phép tính luôn là một vector. Số cột của ma trận phải bằng với số hàng của vector.
Một ma trận m * n nhân với một vector n * 1 sẽ có tích là một vector m * 1
Phân tích
Đầu tiên, ta xoay ngang vector lại thành
Sau đó nhân lần lượt từng dòng của ma trận với :
Cuối cùng lấy tổng của từng hàng:
Phép nhân ma trận – vector trong NumPy
Trong NumPy, để nhân ma trận với vector như trên, ta có thể dùng:
Matrix_name.dot(vector)
Từ phiên bản 3.5 trở lên Python đã hỗ trợ toán tử @:
Matrix @ vector
Để hiểu rõ hơn, chúng ta cùng đi đến Ví dụ:
import numpy as np
_a = [ [ 1, 2 ], [ 3, 4 ], [ 5, 6 ] ]
a = np.array(_a) #Create a 3 * 2 matrix
_b = [ 1, 2 ]
b = np.array(_b) #Create a 2-dimension vector
print(a)
print(b)
print(‘a * b:’, a.dot(b)) #print out a * b using narray.dot()
print(‘a * b:’, a @ b) #print out a * b using @ operation
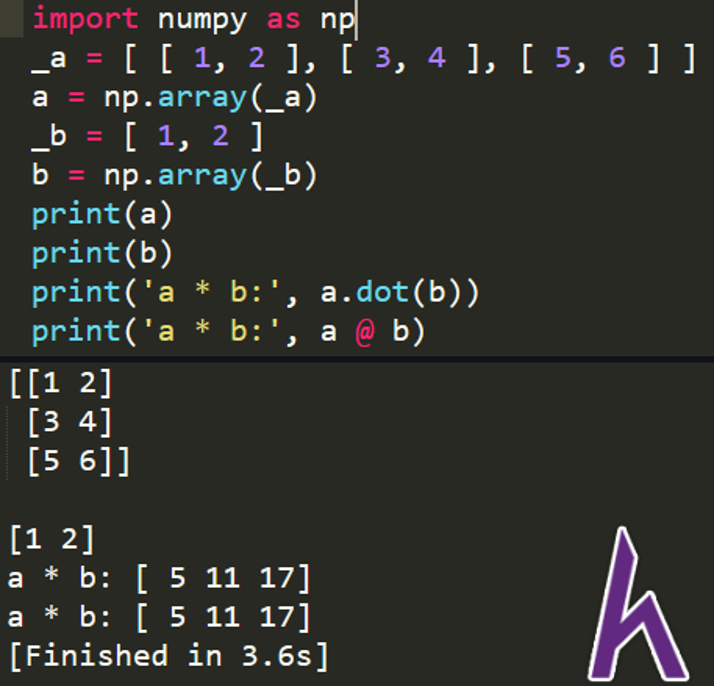
Thực hiện từng bước:
Đầu tiên xoay ngang b:
Nhân từng dòng a với b:
Kết quả phép nhân là tổng từng dòng
Nhân ma trận với ma trận
Chúng ta nhân 2 ma trận bằng cách tách 1 ma trận ra thành nhiều vector rồi nhân, sau đó ghép các kết quả lại.
Để nhân 2 ma trận, số cột của ma trận 1 phải bằng số hàng ở ma trận 2.
Một ma trận m * n nhân với một ma trận n * o sẽ cho kết quả là một ma trận m * o
Phân tích
Đầu tiên tách ma trân thứ 2 thành 2 vector nhỏ: thành
và
Nhân ma trận đầu lần lượt với 2 vector và
:
;
;
Kết quả là 2 vector có cùng kích thước: và
Cuối cùng, ghép 2 vector lại với nhau:
Phép nhân ma trận – ma trận với NumPy
Cũng như nhân ma trận với vector, trong NumPy ta có thể dùng:
Matrix1.dot(matrix2)
Hoặc
Matrix1 @ matrix2
Ví dụ:
import numpy as np
_a = [ [ 1, 2 ], [ 3, 4 ], [ 5, 6 ] ]
a = np.array(_a) #Create a 3 * 2 matrix
_b = [ [1, 3], [2, 1] ]
b = np.array(_b) #Create a 2 * 2 matrix
print(a)
print(b)
print(‘a * b:’, a.dot(b)) #print out a * b using narray.dot()
print(‘a * b:’, a @ b) #print out a * b using @ operation

Thực hiện từng bước:
Đầu tiên tách ma trân thứ 2 thành 2 vector nhỏ: thành
và
Nhân ma trận đầu lần lượt với 2 vector và
:
Kết quả là 2 vector có cùng kích thước: và
Cuối cùng, ghép 2 vector lại với nhau:
Tính chất của phép nhân ma trận
Phép nhân ma trận không có tính chất giao hoán.
Phép nhân ma trận có tính chất kết hợp.
Identity matrix (ma trận đơn vị)
Identity matrix là ma trận mà khi nhân với bất kì ma trận khác cùng kích thước, ma trận đó sẽ không đổi. Phép nhân với identity matrix có tính chất giao hoán. Chúng ta có thể xem identity matrix là “số 1” của ma trận.
Cấu trúc của identity matrix là 1 ma trận có số 1 trên đường chéo.
Ví dụ:
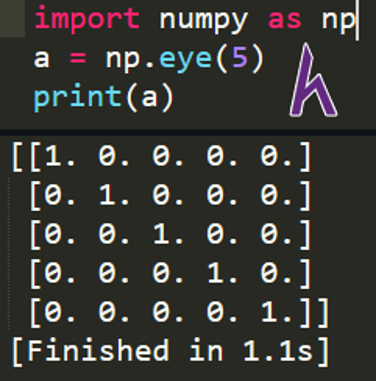
Ta có thể tạo một identity matrix trong NumPy bằng hàm eye:
np.eye(x)
Với x là kích thước của identity matrix.
Ví dụ:
import numpy as np
a = np.eye(5)
print(a)
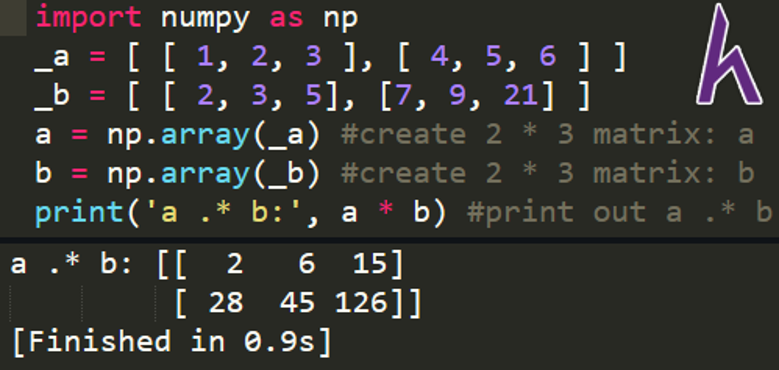
Phép nhân “element-wise” với ma trận
Đối với phép nhân element-wise, kết quả sẽ là một ma trận với những phần tử là tích của các phần tử là tích của 2 phần tử tương ứng trong 2 ma trận.
Với NumPy, ta có thể thực hiện phép nhân element-wise bằng toán tử *
Ví dụ:
import numpy as np
_a = [ [ 1, 2, 3 ], [ 4, 5, 6 ] ]
_b = [ [ 2, 3, 5], [7, 9, 21] ]
a = np.array(_a) #create 2 * 3 matrix: a
b = np.array(_b) #create 2 * 3 matrix: b
print(‘a .* b:’, a * b) #print out a .* b
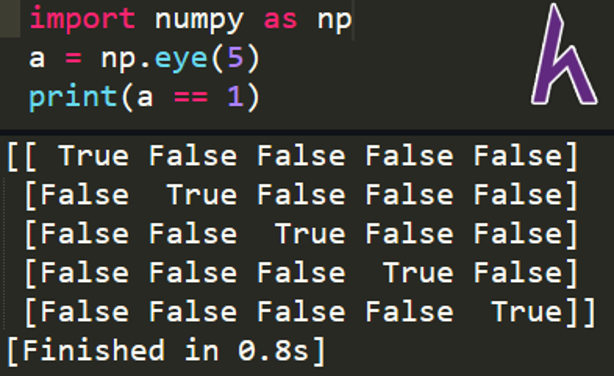
Toán tử logic với ma trận
Ta hoàn toàn có thể thực hiện các toán tử logic với ma trận. Kết quả trả ra sẽ được ghi vào một ma trận với kích thước tương đương.
Ví dụ:
import numpy as np
a = np.eye(5)
print(a == 1)
Inverse matrix (ma trận khả nghịch)
Inverse matrix được kí hiệu bằng: A-1
Tích của ma trận với ma trận đảo của nó sẽ là một Identity matrix.
Tương tự như trong số tự nhiên: 2 * 2-1 = 1
Với NumPy function dùng để invert matrix là:
np.linalg.pinv(matrix)
Ví dụ:
import numpy as np
_a = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
a = np.array(_a)
a_i = np.linalg.pinv(a) #Create inverse of a
print(a_i)
print(a @ a_i)
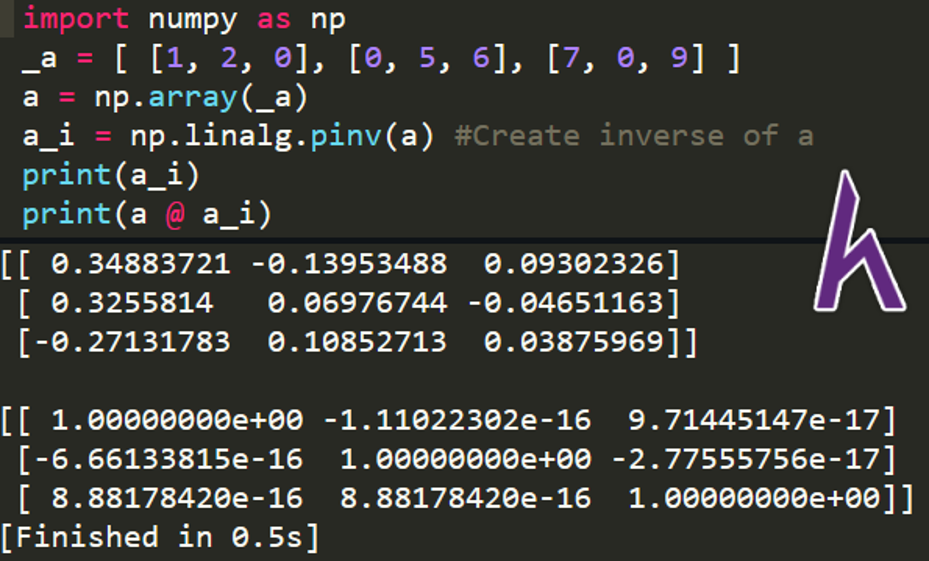
Lưu ý: Identity matrix này hiển thị giá trị rất nhỏ thay cho số 0, ta có thể làm tròn để có identity matrix chính xác. Một số ma trận không thể invert.
Transpose matrix (ma trận chuyển vị)
Transpose matrix được kí hiệu là: AT
Transpose matrix là ma trận đảo hàng và cột so với ma trận gốc.
Với NumPy ta sử dụng function np.transpose() để transpose matrix.
Ví dụ:
import numpy as np
_a = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
a = np.array(_a)
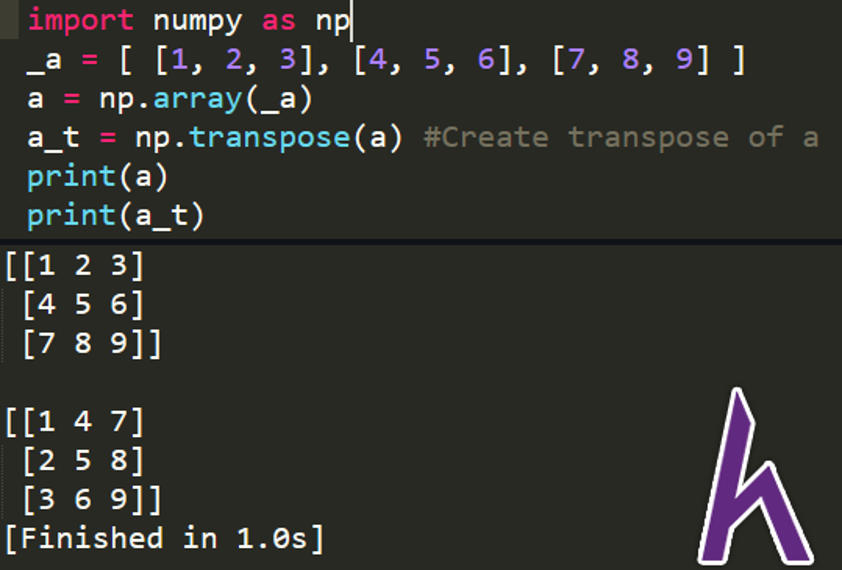
a_t = np.transpose(a) #Create transpose of a
print(a)
print(a_t)
Hàm size với ma trận
Chúng ta có thể sử dụng hàm size để lấy kích thước của ma trận:
np.size(matrix, axis)
Trong đó:
- matrix: ma trận cần tìm kích thước
- axis: chiều, nếu là 0 sẽ trả về số hàng, 1 trả về số cột, mặc định trả về số phần tử.
Ví dụ:
import numpy as np
_a = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
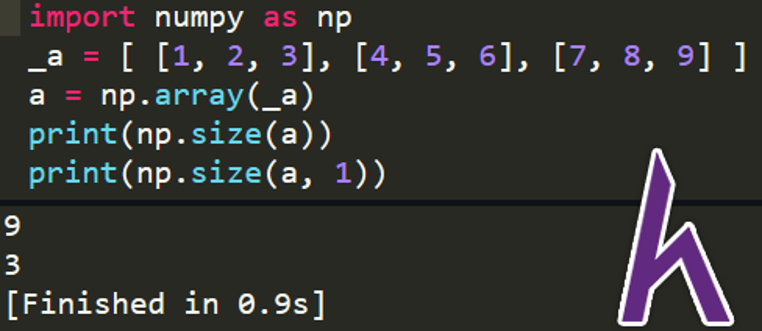
a = np.array(_a)
print(np.size(a))
print(np.size(a, 1))
Hàm sum và max/min với ma trận
Chúng ta có thể sử dụng hàm sum để lấy tổng các phần tử, max để lấy phần tử lớn nhất, min để lấy phần tử nhỏ nhất.
Cấu trúc:
np.sum(matrix,axis)
np.max(matrix,axis)
np.min(matrix,axis)
Trong đó
- matrix: ma trận cần tìm kích thước
- axis: chiều, nếu là 0 sẽ tính theo cột, 1 sẽ tính theo hàng, mặc định sẽ tính trên cả ma trận.
Ví dụ:
import numpy as np
_a = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
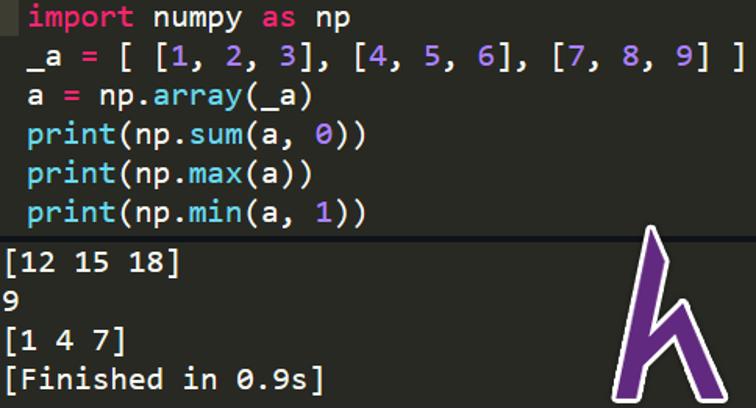
a = np.array(_a)
print(np.sum(a, 0))
print(np.max(a))
print(np.min(a, 1))
Ý nghĩa của ma trận trong Machine Learning
Đối với Machine Learning, chúng ta phải xử lí những dữ liệu với số lượng rất lớn, ta không thể cứ dùng vòng lặp duyệt qua từng dữ liệu được vì sẽ thiếu tối ưu về tốc độ. Vì thế chúng ta cần một công cụ mạnh hơn để xử lí những dữ liệu số lượng lớn, đó là ma trận. Với các phép tính với ma trận, chỉ cần 1 dòng lệnh ta đã có thể cùng lúc thực hiện phép tính trên nhiều dữ liệu.
Kết luận
Bài viết này đã hướng dẫn cho các bạn về ma trận và vector với NumPy.
Ở bài sau, Kteam sẽ giới thiệu về THUẬT TOÁN LINEAR REGRESSION VÀ HÀM HYPOTHESIS
Cảm ơn bạn đã theo dõi bài viết. Hãy để lại bình luận hoặc góp ý của mình để phát triển bài viết tốt hơn. Đừng quên “Luyện tập – Thử thách – Không ngại khó”.
Tải xuống
Tài liệu
Nhằm phục vụ mục đích học tập Offline của cộng đồng, Kteam hỗ trợ tính năng lưu trữ nội dung bài học Ma trận và vector với NumPy dưới dạng file PDF trong link bên dưới.
Ngoài ra, bạn cũng có thể tìm thấy các tài liệu được đóng góp từ cộng đồng ở mục TÀI LIỆU trên thư viện Howkteam.com
Đừng quên like và share để ủng hộ Kteam và tác giả nhé!

Thảo luận
Nếu bạn có bất kỳ khó khăn hay thắc mắc gì về khóa học, đừng ngần ngại đặt câu hỏi trong phần bên dưới hoặc trong mục HỎI & ĐÁP trên thư viện Howkteam.com để nhận được sự hỗ trợ từ cộng đồng.
Nội dung bài viết
Khóa học
Machine Learning cơ bản với NumPy

Với mục đích giới thiệu đến mọi người về Machine Learning cũng như tạo điểm khởi đầu cho các bạn mới, muốn tham gia và tìm hiểu ban đầu về lĩnh vực khá hot này. Cùng Kteam tìm hiểu về Machine Learning cơ bản với ngôn ngữ Python.
Thông qua khóa học MACHINE LEARNING VỚI NUMPY, Kteam sẽ hướng dẫn các kiến thức cơ bản của thuật toán Machine Learning để các bạn có thể tạo ra những sản phẩm Machine Learning của riêng mình.



Nôm na là cái ma trận là cái ma trận trong môn Đại số tuyến tính
Bổ dưỡng lắm các ông ạ.
Mình thuộc loại ngu đần về mảng này nhưng mà xem cái ngu hơn hẳn.
Nói đùa vậy cho vui chứ thực sự hay lắm. Nhờ có HKteam mà mình chập chững có những dòng code đầu tiên để tự động hóa cho công việc của mình.
Cảm ơn rất nhiều!
Kteam ơi, hình như phút thứ 18:27 sai cách tính rồi ạ, phải là 1x7 + 2x9 + 3x21 mới ra 88 và đúng theo quy tắc nhân ạ
Shout out to Howkteam. Dạy kỹ từ căn bản, không phải như kiểu trang web khác. Dạy toàn presume là đã hiểu hết về toán học.
Mình muốn tải nội dung bài giảng về thì phải làm sao ạ?